Cracking Viginere Cipher

Vigenere Cipher
Viginere cipher is a polyalphabetic cipher that encrypts by setting a period based on the key length. Therefore, when the cipher was first developed it was assumed that it would be safe from frequency attacks. However, when an attacker can guess the key length, it is no longer safe from frequency attacks.
Guessing the Key Length
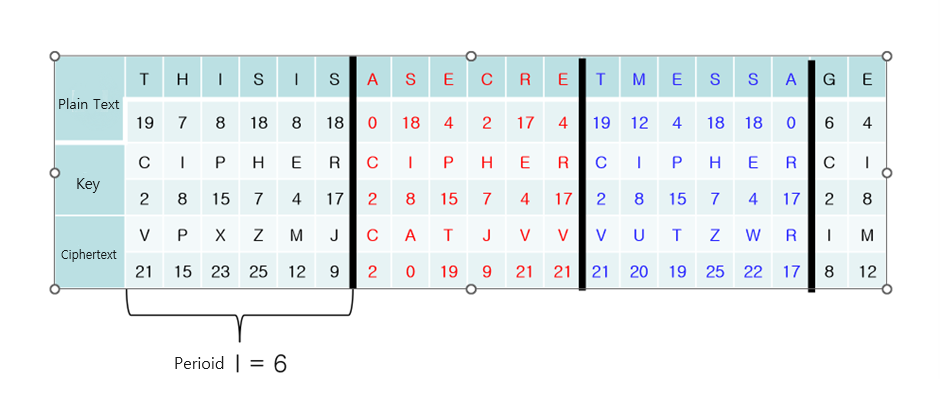
Since Vigenere CIpher is a polyalphabetic cipher, it normally creates different cipher text for the same plain text. For instance, the period of the picture is 6, so the key will be reused once it reaches 6. Therefore, the critical problem is that if the text is located at the same index and it has the same index, it will create the same cipher char.
For instance, in the case of the picture, the first T was ciphered to V, and T from “TMESSA” was also ciphered to “V”.
By these characteristics, an attacker can predict the key length and perform frequency attacks.
Based on this, I wrote a Python code that automatically predicts the key length:
def guess_key_length(encrypted_text):
text_list_org = list(encrypted_text)
text_list_shifted = text_list_org
coincidence_list = list()
coincidence_temp = 0
for i in range(1, 20): # Calculate coincidence for each key length
text_list_shifted = np.roll(text_list_shifted, 1) # Shift the text by 1
for i, j in zip(text_list_org, text_list_shifted):
if (i == j): # If the letters match, increment coincidence
coincidence_temp += 1
coincidence_list.append(coincidence_temp)
coincidence_temp = 0
sorted_list = sorted(coincidence_list, reverse = True)
result_list = list()
result_list.append(coincidence_list.index(sorted_list[0]) + 1)
result_list.append(coincidence_list.index(sorted_list[1]) + 1)
result_list.append(coincidence_list.index(sorted_list[2]) + 1)
result_list.append(coincidence_list.index(sorted_list[3]) + 1)
result_list.append(coincidence_list.index(sorted_list[4]) + 1)
result_list.append(coincidence_list.index(sorted_list[5]) + 1)
return result_list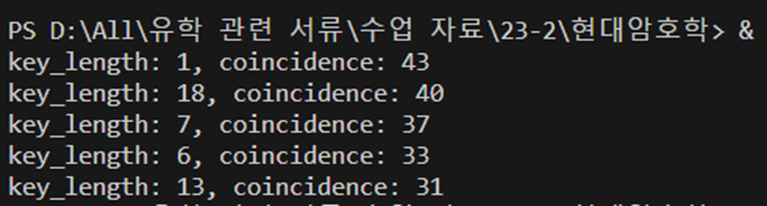
Guessing the Real Key
Now we know the possible key lengths, the only thing left to crack vigenere cipher is getting the key. This is possible by frequency attack.
def get_possible_keys(encrypted_text, key_length):
num = {0: 'a', 1: 'b', 2: 'c', 3: 'd', 4: 'e', 5: 'f', 6: 'g', 7: 'h', 8: 'i', 9: 'j', 10: 'k', 11: 'l', 12: 'm', 13: 'n', 14: 'o', 15: 'p', 16: 'q', 17: 'r', 18: 's', 19: 't', 20: 'u', 21: 'v', 22: 'w', 23: 'x', 24: 'y', 25: 'z'}
alphabets = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z']
alphabets_freq = [0.08167, 0.01492, 0.02782, 0.04253, 0.12702, 0.02228, 0.02015, 0.06094, 0.06966, 0.00153, 0.00772, 0.04025, 0.02406, 0.06749, 0.07507, 0.01929, 0.00095, 0.05987, 0.06327, 0.09056, 0.02758, 0.00978, 0.0236, 0.0015, 0.01974, 0.00074]
encrypted_text_list = list(encrypted_text.lower())
#print(encrypted_text_list)
v1 = 0
blocks = [[] for x1 in range(0, key_length)]
while v1 < key_length:
for i2 in range(v1, len(encrypted_text_list), key_length):
blocks[v1].append(encrypted_text_list[i2]) # i2 += key_length
v1 += 1
# print(blocks) # I made a blocks that groups the ciphers that were encrypted with same key
v1 = 0
key_array = ""
while v1 < key_length:
frequnecy_list = list()
for alphabet in alphabets:
freq_temp = blocks[v1].count(alphabet)
freq_temp = freq_temp / 26 # converting frequency to 0 ~ 1
freq_temp = round(freq_temp, 7)
frequnecy_list.append(freq_temp)
maximum_shift = 24
correlation_scores = list()
t = 0
while maximum_shift >= 0:
shifted_alphabtes_freq = shift_left(alphabets_freq, t)
correlation_score = np.dot(frequnecy_list, shifted_alphabtes_freq) #calculating similarity by dot product
#https://math.stackexchange.com/questions/689022/how-does-the-dot-product-determine-similarity
correlation_score = round(correlation_score, 6)
correlation_scores.append(correlation_score)
maximum_shift -= 1
t += 1
max_correlation_score = max(correlation_scores)
F = [D for D, E in enumerate(correlation_scores) if E == max_correlation_score]
F[0] = ((26 - F[0]) % 26)
key = num[F[0]].upper()
key_array += key
v1 += 1
return key_arrayThe code conducts frequency attack and gives possible keys. The similarity calculation is based on dot productivity.

Result

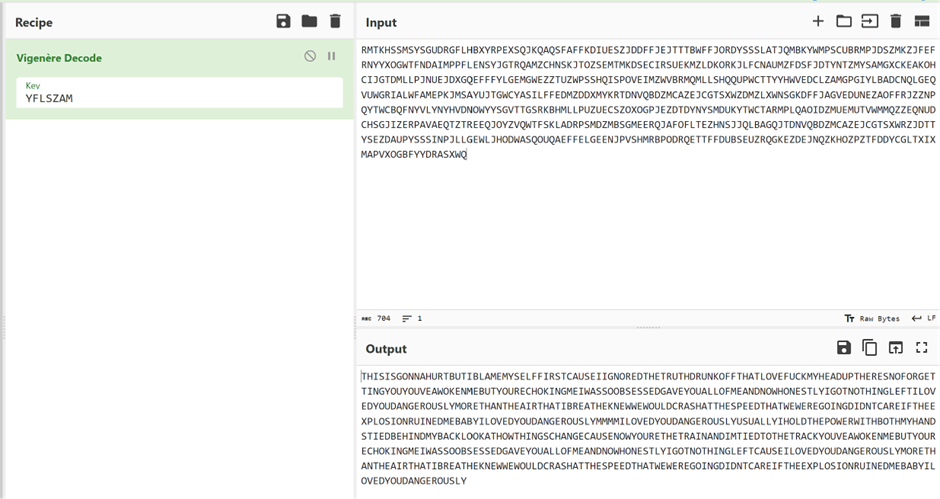
Successfully cracked the cipher!
